I learnt about this strange attractor from Daniel Shiffman and based my research and code off of his video. E. N. Lorenz discovered this 3-dimensional differential equation by simplifying a weather model. The behaviour it exhibits is called "deterministic chaos" (www.math.toronto.edu, n.d.). It's one of the earliest discoveries of the butterfly effect because of the hugely differentiating results based on tiny changes in the initial values used. The plotting of the attractor also looks like a butterfly's wings out of coincidence.
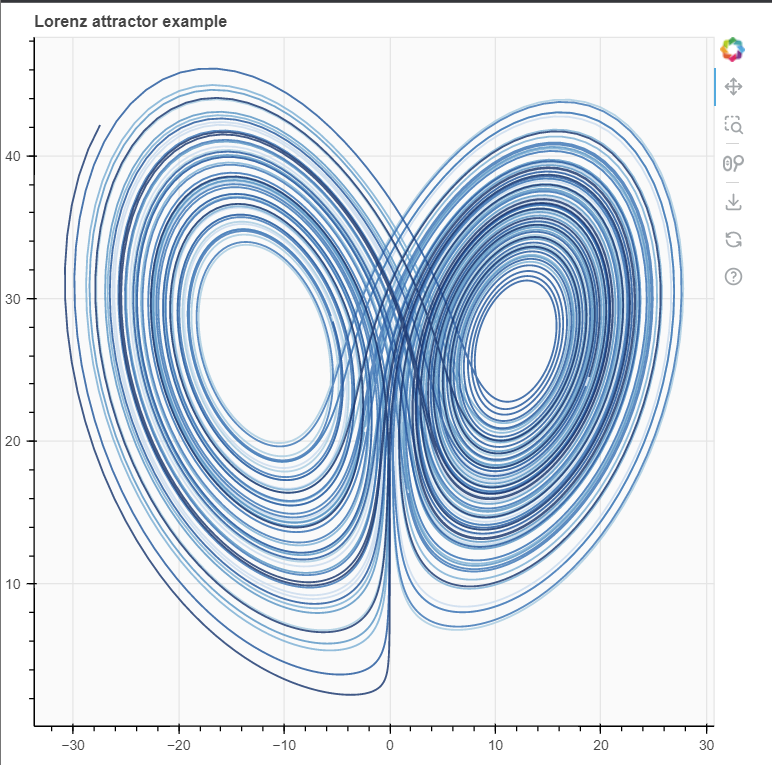
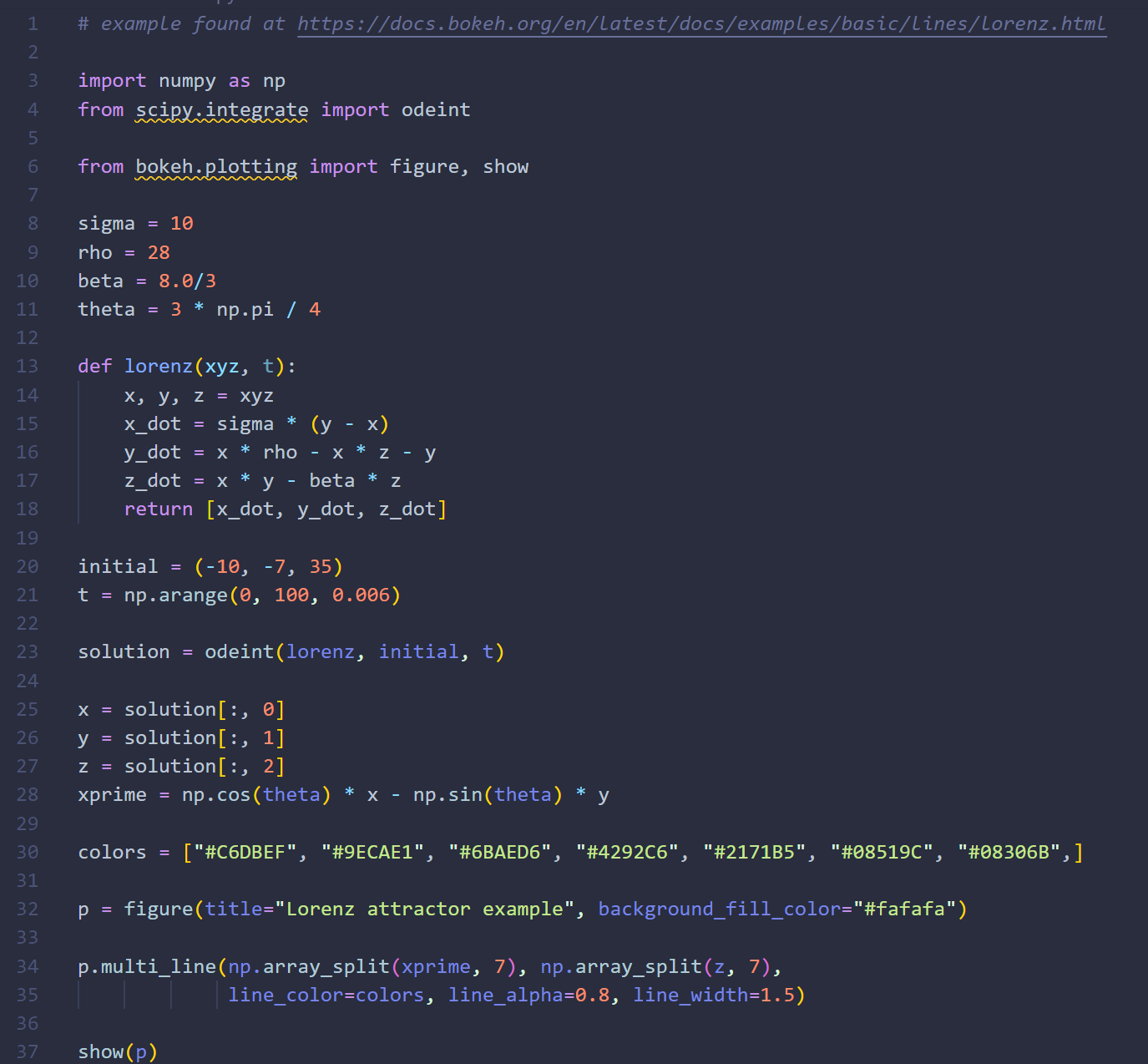
I started out with this plot from the bokeh documentation just to familiarise myself with that library. After some research I realised I didn't want to use graphs in my outcome and so followed Daniel Shiffman's tutorial, modified it, and created the animated plot you see below.
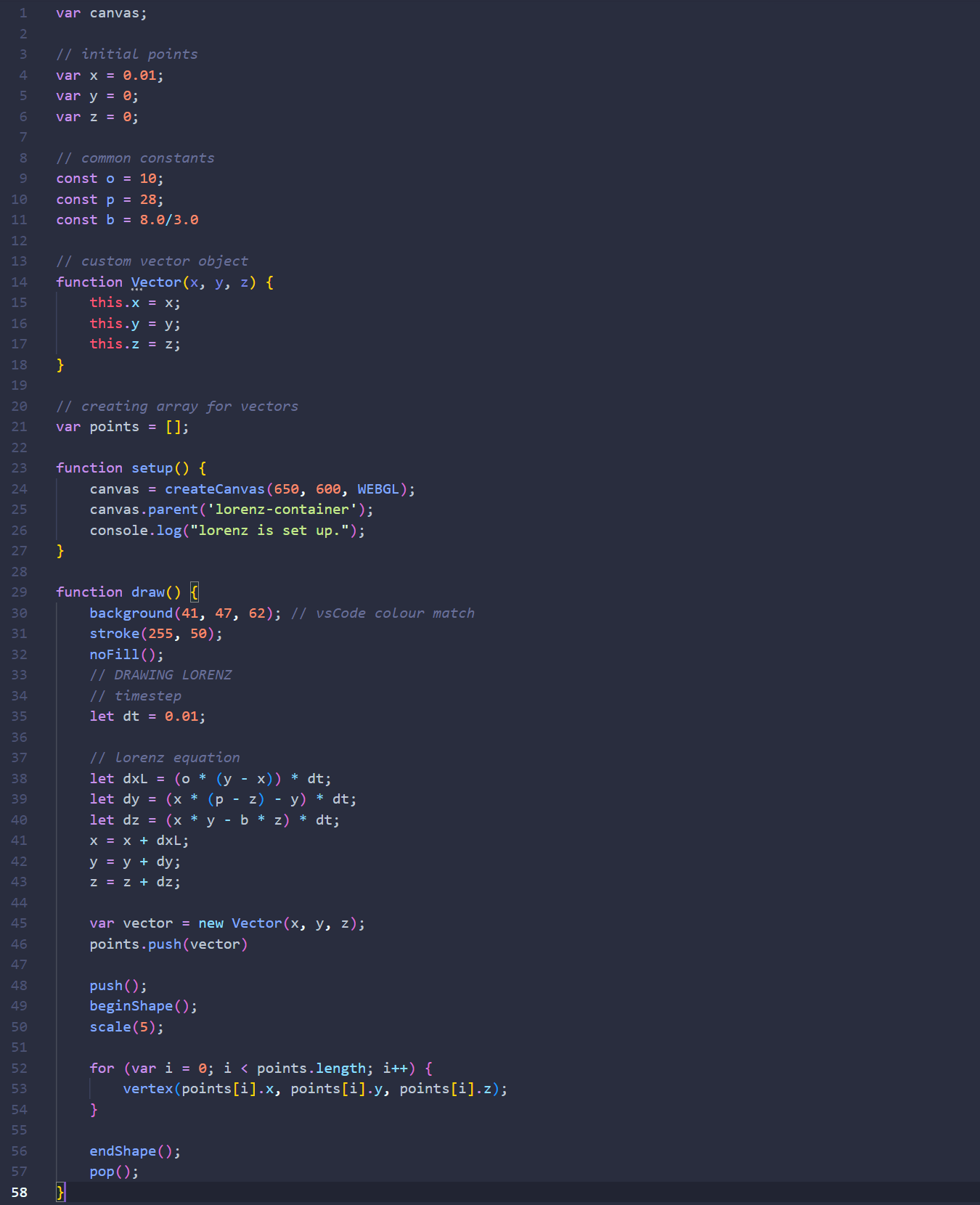
I started out in Processing to be more comfortable and then moved to JavaScript once I felt I knew how the system was working. I was able to borrow the custom Vector object I had created for the Tinker Bell fractal. I like how the line moves because the slight variations give it life. The overall shape is also reminiscent of the bell of a jellyfish.